Sistemas y procesos multivariables
Este artículo es la primera parte de una serie de cuatro. Parte 2. Parte 3. Parte 4.
En muchos procesos industriales, el objetivo del sistema de control consiste en mantener más de una variable en su punto de ajuste (valor de referencia o set point). este tipo de casos se consideran como sistemas de control multivariable. La presencia de las interacciones entre lazos o dinámicas hará que el desempeño de un lazo afecte a los otros y viceversa. En otras palabras, la interacción complica la sintonía de los lazos de manera independiente.
En los procesos industriales y en la mayoría de los problemas de control hay varias variables que deben ser controladas y una variedad de variables para manipular. En casi cualquier proceso industrial importante hay por lo menos dos variables que deben ser controladas: la calidad del producto y su cantidad (Seborg, Edgar, & Mellichamp, 1989).
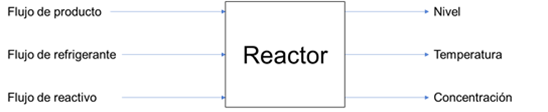
Supóngase, por ejemplo que se desea controlar el nivel, la temperatura y la composición en un reactor químico. Si se toman como variables manipuladas el flujo de la corriente del producto, el flujo del refrigerante y el flujo de reactivo, se obtiene entonces un diagrama de bloques como el mostrado a continuación:
Los sistemas lineales MIMO pueden representarse al igual que los sistemas SISO en el dominio del tiempo mediante ecuaciones diferenciales en el espacio de estados. En el caso de un sistema MIMO con entrada u(t) ∈ , estados
y salida y(t) ∈
, su modelo en el espacio de estados se puede escribir como:
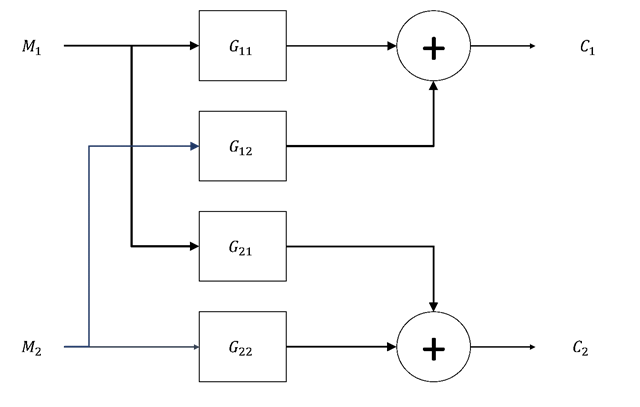
También los sistemas multivariables pueden representarse a través de funciones de transferencias. En este caso, la representación no corresponde a una sola función de transferencia. En vez de eso, la representación corresponde a una matriz de funciones de transferencias.
En general, la conversión de las ecuaciones (1) y (2) de la representación en espacio de estado a la representación matricial de funciones de transferencia requiere la aplicación de la transformada de Laplace obteniéndose
Si el sistema estuviera descrito en variables de desviación (es decir, que )
Ejemplo 1:
Considérese el proceso descrito por la siguiente ecuación en espacio de estados:
Entonces, puede llamarse
y con esto se escribe que
y la representación matricial puede calcularse de la siguiente forma
Luego
Esta representación puede quedar más clara al sustituir nuevamente el vector que representa a las variables involucradas
CUIDADO. Véase que estas últimas expresiones dependen simultáneamente de t y s. Esto es "incorrecto" en el sentido matemático. Es una manera de representar la expresión, en donde se debe entender que, para escribir una representación explícita, es necesario aplicar correctamente la transformada inversa de Laplace. En este caso, lo "correcto" en el sentido matemático sería escribir a como
. En muchos libros se encuentran expresiones como las mostradas, y debe entenderse correctamente, en el sentido que la variable s representa a un operador (operador derivada, a veces representado por la letra p), y no a una variable en el sentido estricto.
Con esto se tiene que y depende de u según
Véase que cada una de las salidas dependen de cada una de las entradas
. Además, véase que existe una respuesta libre, no dependiente de las entradas, debido a la presencia de condiciones iniciales no distintas de cero.
Ir a:
Segunda parte: Interacción entre variables dinámicas
Tercera parte: Diseño de controladores para un sistema multivariable – una introducción
Cuarta parte: Procedimiento de diseño de un sistema de control multivariable (primer acercamiento)
Referencias:
Seborg, D. E., Edgar, T. F., & Mellichamp, D. A. (1989). Process Dynamics and Control. John Wiley & Sons.
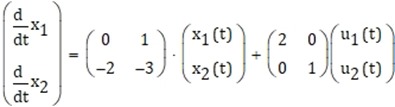
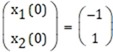
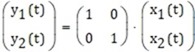
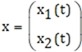
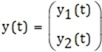
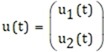
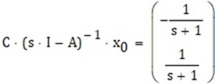
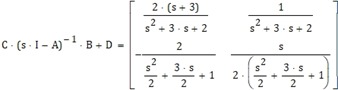
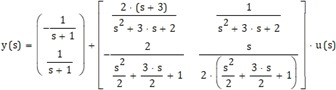
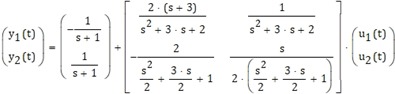
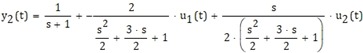


Comentarios
Publicar un comentario