Modelos de un sistema

El modelo de un sistema es una descripción de él, como el enlace entre la teoría y la realidad. El sistema corresponde a una realidad que no es presentada al observador sino que debe ser reconocido por él. Un sistema no corresponde a un objeto del mundo real sino a una forma de organizar la percepción humana de las cosas que forman parte del mundo real. Para esto, hay varios puntos de vista filosóficos: el punto de vista constructivista de la realidad (Skyttner, 2001) expone que un sistema no existe en el mundo real sino en la mente humana. Otro punto de vista, el ficcionalista, indica que el concepto de sistema puede usarse para el propósito en el que es pensado a pesar de que sea incorrecto o presente contradicciones con una situación específica (Skyttner, 2001).

Para darle sentido a la descripción de sistemas, se utilizan modelos, que permiten visualizar los fenómenos que de alguna manera representan o describen al sistema en cierta medida. Los modelos pueden ser de muchos tipos, como miniaturas, versiones simplificadas o a escalas del sistema real. Los modelos pueden ser usados para interpretar a los sistemas y entenderlos con mayor facilidad, para la predicción de consecuencias luego de aplicadas algunas acciones o para ejecutar acciones que pueden ser muy costosas de aplicar, o difíciles, en el sistema real.

En particular, los modelos matemáticos permiten describir a un sistema usando ecuaciones o sistemas de ecuaciones. Esto en sí presenta algunas simplificaciones, pero el modelo puede hacerse tan complicado que no pueda utilizarse en alguna forma, o no puedan hallarse soluciones numéricas para él, si eso es lo que se desea. La matemática es un área de conocimiento amplia, y puede usarse para representar e interpretar muchas interacciones, y por lo general obtener un modelo de un sistema no es un trabajo sencillo. Los modelos matemáticos pueden ser de distinta naturaleza, dependiendo de la teoría que los describe o sustenta.

Systemas y Modelos

La teoría general de sistemas es el nombre que se la da a la descripción y construcción de modelos teóricos que abarca desde la construcción matemática hasta la teoría especializada de la disciplina del conocimiento en el cual se aplica. (Boulding, 1956). En cierta medida, la matemática intenta hacer una descripción de las relaciones altamente general de las relaciones en un sistema coherente que no necesariamente tiene una conexión con el mundo real, ya que estudia todas las relaciones abstractas que puedan pesarse sobre una situación concreta, ya sea de manera cuantitativa (cálculo diferencial, integral, algebraico y otros) o en análisis cualitativo (lógica difusa, redes neuronales artificiales, computación inteligente y otros). Sin embargo, la matemática contiene a la vez a todas las teorías y a ninguna, es decir, es el lenguaje de la teoría pero no da ningún contexto. Por el otro lado, las diversas disciplinas de las ciencias poseen una descripción parcial del universo. La teoría general de sistemas intenta integrar ambos acercamientos.

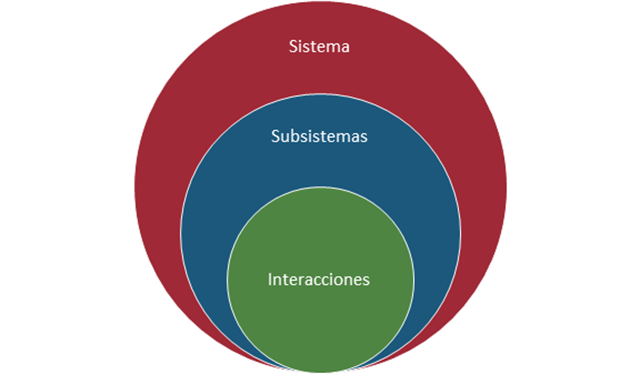
Un sistema es un todo que consiste en elementos o subsistemas (Elnashaie, 2003). El concepto de sistemas y subsistemas es relativo, y depende del nivel del análisis utilizado. El sistema tiene una frontera que lo diferencia de sus alrededores, y puede intercambiar información de algún tipo con sus alrededores (por ejemplo, en un proceso químico, puede intercambiar masa, calor, trabajo). Un sistema es descrito por sus subsistemas y su interacción con los alrededores, y estos elementos pueden ser elementos materiales o procesos que ocurren dentro de las fronteras del sistema, o bien, pueden ser ambos, dependiendo de lo compleja que sea su interacción (Elnashaie, 2003).

Una definición de modelo, dada en (Fasol & Jörgl, 1980), es una copia reducida de un sistema original siguiendo las leyes de similitud del modelo o una analogía. Se entiende de un modelo físico como un objeto, un circuito, o algo equivalente que se comporta exactamente o al menos comparablemente con el original. Un modelo matemático, en cambio, representa las relaciones entre las variables físicas del sistema a través de estructuras matemáticas como ecuaciones algebraicas simples, ecuaciones diferenciales o un sistema de ecuaciones diferenciales. Un modelo matemático intenta poner la realidad de un sistema físico en una forma matemática aceptable (Elnashaie, 2003).

Según (Hawking, 1989), una teoría es un modelo del universo o de una parte de él, junto a un grupo de reglas que relacionan cantidades en el modelo a las observaciones que se hacen de él. Solo existe en la mente humana y no posee otra realidad. Una buena teoría satisface dos requerimientos: describe precisamente a un gran número de observaciones al compararse con el modelo y predice de manera finita los resultados de futuras observaciones.

Referencias

Boulding, K. E. (1956). General Systems Theory - The Skeleton of Science. Management Science, 2(3), 197-208.

Elnashaie, S. S. (2003). Conservation Equations and Modeling of Chemical and Biochemical Processes. New York: Marcel Dekker, Inc.

Fasol, K. H., & Jörgl, H. P. (1980). Principles of Model Building and Identification. Automatica, 16, 505-518.

Hawking, S. (1989). A Brief History of Time: From The Big Bang to Black Holes. London: Bantam Press.

Skyttner, L. (2001). General Systems Theory. Singapore: World Scientific Printers.