Interacción entre variables dinámicas
Este artículo es la segunda parte de una serie de cuatro. Parte 1. Parte 3. Parte 4.
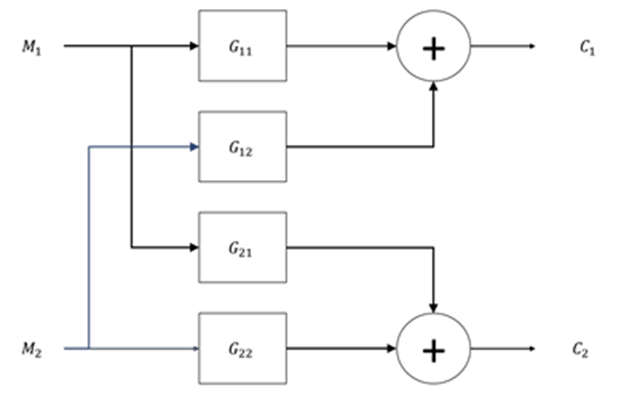
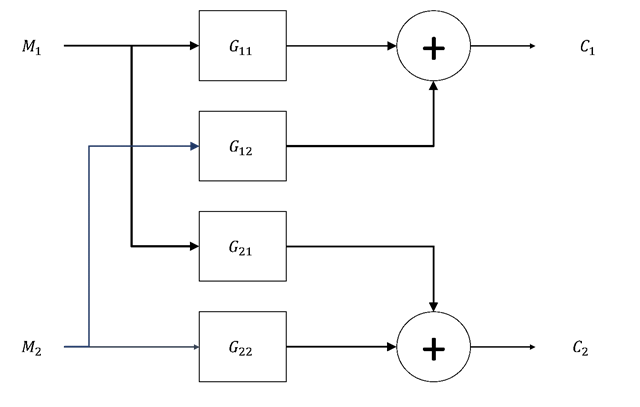
En los sistemas multivariables la interacción entre variables es el efecto más importante en el diseño y sintonía de los lazos de control. Se dice que un proceso presenta interacciones dinámicas cuando una variable de entrada afecta a más de una variable de salida. Es decir, que, para un par definido variable de entrada y variable controlada, no sólo la variable controlada se aleja o se acerca a su punto de ajuste en virtud de cambios en la variable de entrada (Luyben & Luyben, 1997). La figura muestra un diagrama de cómo es la interacción dinámica.El sistema representado en la figura tiene la siguiente representación matricial
Véase que esta representación matricial relaciona a cada una de las variables de entrada M con cada una de las variables de salida C, lo que significa que cada entrada afecta a cada salida. Cuando existen interacciones entre las variables, cada variable manipulada puede afectar a varias variables controladas (Seborg, Edgar, & Mellichamp, 1989).
Para establecer una estrategia adecuada de control para un sistema multivariable, es necesario considerar las interacciones adecuadamente y la selección apropiada de las variables manipuladas y su apareamiento con las variables controladas puede no ser obvia. Se puede ver claramente que cada una de las entradas (M1, M2) tiene influencia sobre cada una de las salidas (C1, C2). La magnitud de tal influencia depende de las ganancias de las funciones de transferencia.
Los sistemas multivariables interactuantes son frecuentes en la industria de procesos y por su misma naturaleza plantean problemas en el control automático de los mismos. Basta mencionar el proceso de destilación, donde las composiciones de destilado y de fondo se configuran con las variables de entrada, caudal de reflujo en el tope y flujo de calor al rehervidor (reboiler) un sistema de dos por dos interactuante.
Dado que la interacción deteriora notablemente el comportamiento de los sistemas controlados, se han diseñado estrategias para un mejor manejo de estos. Uno de los procedimientos es el apareamiento selectivo de las variables por el método de la matriz de ganancias relativas; con resultados óptimos en los casos en que existe una configuración de ganancias favorable, siendo menos conveniente a medida que las ganancias se apartan de los valores ideales, casos para los que son necesarias otras estrategias que se comentarán en próximos posts.
Ir a:
Primera Parte: Sistemas y procesos multivariables
Tercera parte: Diseño de controladores para un sistema multivariable – una introducción
Cuarta parte: Procedimiento de diseño de un sistema de control multivariable (primer acercamiento)
Referencias:
Luyben, W. L., & Luyben, M. L. (1997). Essentials of Process Control. Singapore: McGraw-Hill.
Seborg, D. E., Edgar, T. F., & Mellichamp, D. A. (1989). Process Dynamics and Control. John Wiley & Sons.
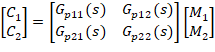


Comentarios
Publicar un comentario