Procedimiento de diseño de un sistema de control multivariable (primer acercamiento)

Este artículo es la cuarta y última parte de una serie. Parte 1. Parte 2. Parte 3.

Basado en lo analizado en los artículos anteriores, el siguiente procedimiento indica como debe hacerse el diseño de un sistema de control diagonal (también llamado descentralizado). Este procedimiento será completado posteriormente al incluir otros criterios para el diseño en lecturas posteriores.

Procedimiento 1: Diseño de sistema de control multivariable diagonal (descentralizado).

1. Elegir el apareamiento de las variables.

2. Sintonizar cada controlador en cada lazo manteniendo a los otros lazos en modo manual (o lo que es lo mismo, sin controlador).

3. Cerrar todos los lazos (o lo que es lo mismo, activar simultáneamente todos los lazos).

4. Si hay problemas de estabilidad, reducir la ganancia o incrementar el tiempo integral de los controladores en los lazos menos importantes.

Ejemplo: Diseño de un sistema de control descentralizado

Sea el sistema multivariable descrito por la siguiente matriz de funciones de transferencia:

Cada función de transferencia dentro de la matriz puede escribirse en la forma de una función de primer orden más tiempo muerto

Donde T es la constante de tiempo del sistema, K es la ganancia y tm es el tiempo muerto. Se desea diseñar el sistema de control PI descentralizado para este proceso.

Elección del apareamiento.

En este problema, se elige el apareamiento que produzca un mayor efecto sobre la variable controlada (Y) respecto a un cambio en la variable manipulada (U). Aunque esto puede hacerse de forma más sistemática, por ahora esta selección será suficiente. Para esto, puede notarse que U1 tiene una ganancia mayor sobre Y1 (la ganancia vale 1) que U2 (la ganancia vale 0.5). Luego, el apareamiento será U1:Y1 y U2:Y2 (por el mismo motivo).

Variable controlada	Variable manipulada
Y1	U1
Y2	U2

Sintonización de cada controlador

Para la sintonización de cada controlador, se elige un método de sintonización adecuado. En este particular, (O'Dywer, 2009) recoge los métodos de diseño de controladores para distintos tipos de procesos. En particular, en la página 33, si el modelo es uno de primer orden más tiempo muerto (FOLPD), el diseño de un controlador PI ideal puede calcularse como

Modelo del proceso
Forma del controlador	PI Ideal
Autor del método	Lipták (2001)

Para el cálculo, véase que:

Usando el apareamiento seleccionado y el método de diseño seleccionado, se tiene que

Cerrar todos los lazos

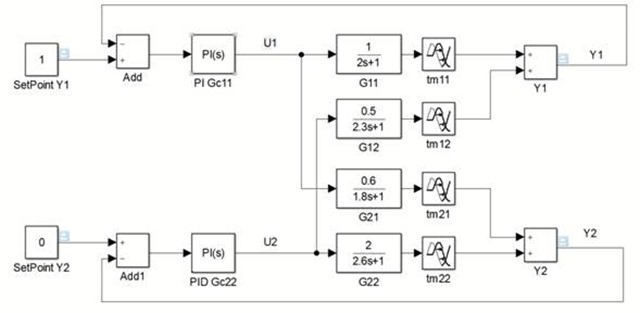
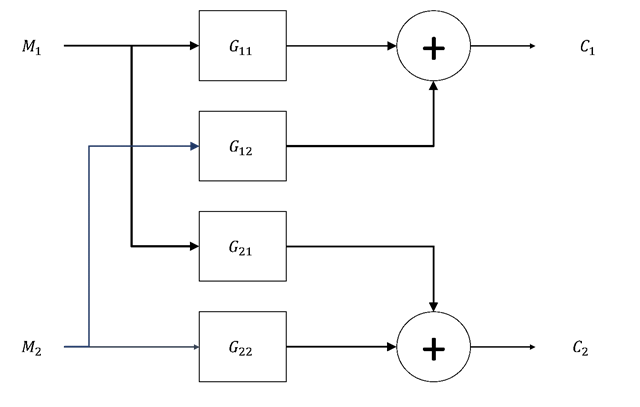
El cierre de todos los lazos se hace en el ambiente de simulación (o en el proceso). En este caso, se presenta el diagrama de bloques en SIMULINK/MATLAB para este ejemplo en la Figura 1.

Figura 1. lazo de control diagonal multilazo (SIMULINK)

Observaciones:

· Los controladores PID de MATLAB pueden configurarse de distinta forma, usando una estructura ideal, paralela, etc. En particular, en este ejemplo, la fórmula del controlador "PI ideal" requerida por MATLAB es

y es evidente que P corresponde al valor de Kc calculado, sin embargo, el tiempo integral del controlador debe ser convertido de forma que .

La implementación en MATLAB requiere representar el tiempo muerto en un bloque aparte. Por eso, cada función de la matriz de funciones de transferencia fue descompuesta en una parte racional y un tiempo muerto. El bloque seleccionado en Matlab para esta representación es el Transport Delay (retardo de transporte).

La activación de estos lazos corresponde entonces a la implementación de estos bloques en Simulink. Véase que ambos lazos están cerrados.

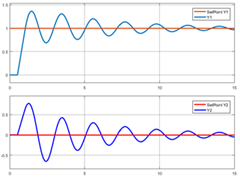
La simulación dinámica de la Figura 2 muestra el comportamiento de los lazos.

(a)	(b)

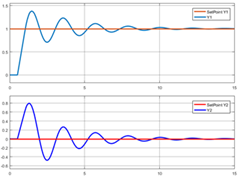
Figura 2. respuesta del sistema de control diagonal multilazo: a) Para cambio en el setpoint de Y1 (sin cambiar el de Y2) y b) para cambio en el setpoint de Y2 (sin cambiar el de Y1)

Para esta simulación, se prueba el comportamiento de cada lazo manteniendo el otro en el punto de operación 0. Cuando se observa el comportamiento de cada lazo, al cambiar el set point de una de las variables, ambas se ven afectadas y cada controlador intenta regresarlas a su valor deseado. Este es el procedimiento recomendado para comprobar el comportamiento de los lazos: realizar un cambio a la vez en cada lazo regresando los otros set points a cero, a fin de identificar más fácilmente de donde proviene el cambio; nunca realice más de un cambio a la vez para hacer un estudio del comportamiento de un lazo.

Puede verse que la respuesta de cada variable es estable, pero subamortiguada. En particular, la respuesta de cada variable es oscilatoria y podría mejorarse esto al disminuir la ganancia proporcional de cada lazo.

Ajuste fino para reducir los problemas de estabilidad.

Para reducir el comportamiento oscilatorio de estos lazos, se recomienda disminuir la ganancia proporcional e incrementar el tiempo integral del controlador menos importante. Cuidado: a veces inclusive al disminuir estos parámetros del menos importante, es posible que el otro lazo siga siendo inestable y pueda ser necesario corregir también el del lazo más importante.

En general, esto corresponde a una sintonización de ensayo y error. Cualquier procedimiento puede servir para lograr esto. Lo que se hará aquí es:

1) disminuir la ganancia proporcional en un 10% del valor actual. Si la respuesta no es la deseada ir a 2.

2) Incrementar el tiempo integral en 10%. Si la respuesta no es la deseada, volver a 1.

Esto que se indica es solo una recomendación. Puede hacerse sobre los dos lazos, pero primero debe hacerse en el menos importante y si no se produce ninguna mejora, ir al más importante.

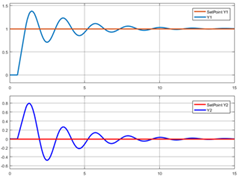
Como este es un ejemplo (y no un caso real), se elegirá el lazo 2 (Y2 vs U2) como lazo menos importante. Al realizar este procedimiento sobre el sistema propuesto (solo sobre la variable de lazo menos importante) la respuesta dinámica presentada fue la de la Figura 3.

(a)	(b)

Figura 3. respuesta del sistema de control diagonal multilazo luego del ajuste fino: a) Para cambio en el setpoint de Y1 (sin cambiar el de Y2) y b) para cambio en el setpoint de Y2 (sin cambiar el de Y1)

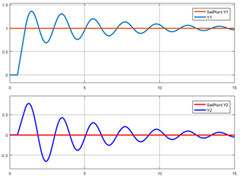
Puede ser difícil observar los cambios al comparar estas figuras. Por ello, se presenta en la Figura 4 una comparación para el cambio en el set point de Y1 antes y después del ajuste fino. Véase que ahora el tiempo de estabilización del lazo 1 es menor y que las oscilaciones son de menor magnitud que antes del ajuste fino.

(a)	(b)

Figura 4. respuesta del sistema de control diagonal multilazo para cambio en el setpoint de Y1: a) antes del ajuste fino y b) luego del ajuste fino.

Una mejor comparación puede hacerse observando el comportamiento de ambas curvas en el mismo gráfico. Esto se muestra en la Figura 5. Si se continuara el procedimiento (o se hicieran cambios en el controlador del lazo 1, se podría mejorar la respuesta.

Figura 5. respuesta del sistema de control diagonal multilazo para cambio en el setpoint de Y1 antes y después del ajuste fino.

Ir a:

Primera Parte: Sistemas y procesos multivariables

Segunda parte: Interacción entre variables dinámicas

Tercera parte: Diseño de controladores para un sistema multivariable – una introducción

Referencias

O'Dywer, A. (2009). Handbook of PI and PID Controller Tuning Rules. London: Imperial College Press.