Diseño de controladores para sistemas multivariables – Una introducción

Este artículo es la tercera parte de una serie de cuatro. Parte 1. Parte 2. Parte 4.

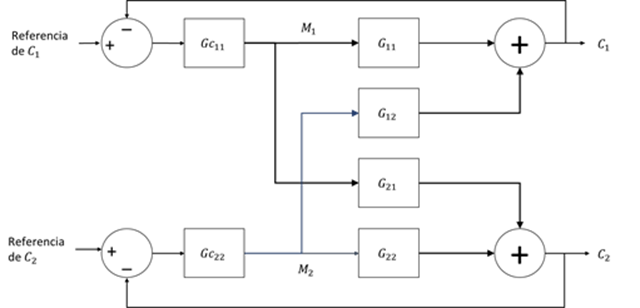
La mayoría de los sistemas de control industrial utilizan la estructura de control diagonal multilazo SISO, pudiendo ser usada por los operadores e ingenieros de planta cuando sea necesario sin requerir de un experto en matemáticas aplicadas (Luyben & Luyben, 1997). Una estructura de control diagonal multilazo se presenta en la figura.

Véase que, en este sistema de control, se decidió controlar a manipulando a a través del controlador , que puede ser uno PI. De la misma manera, se controla a manipulando a a través de .

Aunque no es evidente de la figura, si la elección se hiciera de otra forma, los nombres de las variables del proceso podrían reetiquetarse para representarse de la forma que se muestra. La cuestión de interés ahora es cómo elegir cual es la variable manipulada adecuada para el control de cada una de las variables de interés. Los pasos para llevar a cabo el diseño del sistema de control de acuerdo a dicha estructura son los siguientes (Luyben & Luyben, 1997):

1. Selección de las variables controladas: Esta selección puede realizarse a través de distintas herramientas: la primera de ellas es el juicio de ingeniería. El entendimiento del proceso conduce a una selección lógica de la variable de se desea controlar de acuerdo con las consideraciones económicas, de seguridad, restricciones y la disponibilidad de sensores para tal fin. Muchas veces, la selección de la variable a controlar es obvia, sin embargo, en algunos casos tal selección dependerá de un conocimiento profundo del proceso y sus relaciones con otros.

2. Selección de las variables manipuladas: Una vez que las variables controladas han sido especificadas, la estructura del controlador dependerá de la selección de las variables manipuladas. Para un proceso específico, la selección de las variables manipuladas producirá diferentes estrategias de control. Se desea establecer la variable manipulada que permita mayor lejanía de la singularidad, es decir, que permita controlar el proceso lejos de la inestabilidad.

3. Eliminación de apareamientos incompatibles o pobres: Para eliminar las variables que, al elegirse, produzcan desestabilización del proceso, se pueden usar distintos criterios. Uno de ellos es el criterio de Arreglo de Ganancia Relativa (RGA, por sus siglas en inglés Relative Gain Array).

4. Encontrar el diseño del controlador: Para sintonizar un sistema de control PI en un arreglo diagonal con N variables controladas, se deben elegir 2N parámetros para controladores PI, tales que el sistema global sea estable y produzca una respuesta aceptable.

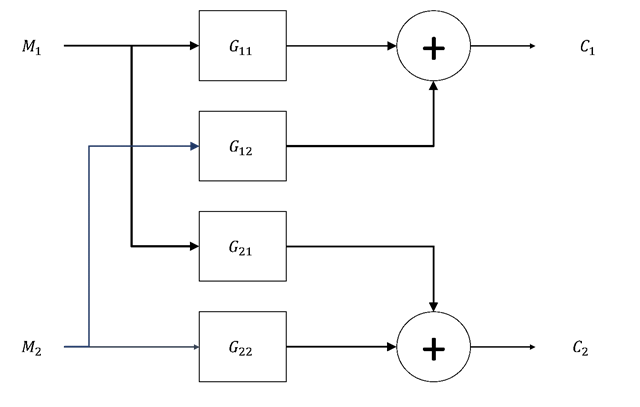
Véase un concepto que ha aparecido varias veces en los últimos párrafos: el concepto de arreglo diagonal. Se comentó que en la figura el arreglo es diagonal, pero no se ha indicado por qué. Véase que, como se comentó antes las funciones de transferencia del proceso se representan como

 

Aquí puede verse que el proceso está representado por una matriz que contiene cuatro funciones de transferencia que corresponden al sistema multivariable. Esta matriz se conoce como matriz de funciones de transferencia:

 

Así como puede representarse al proceso a través de una matriz de funciones de transferencia, los controladores también corresponden a un arreglo matricial. En particular, un sistema de control multivariable es diagonal, como el caso que se presenta, cuando su matriz de funciones de transferencia es

 

O, lo que es equivalente, que las variables manipuladas son activadas por el controlador a través del error del lazo, definido como

 

Esta representación está formada por dos controladores, , lo cual hace que la matriz que representa al sistema de control sea diagonal.

El procedimiento descrito en Luyben & Luyben (1997), consiste entonces en diseñar, para un sistema de 2x2, un sistema de control dado por esta representación diagonal. Y el problema de diseño es elegir cual es la variable adecuada para tal tarea. Inicialmente en este blog solo se usarán criterios de ingeniería para el diseño de estos controladores. Más adelante se comentará la selección a través del método de arreglo de ganancias relativas o se recurrirá al diseño de desacopladores dinámicos.

Ir a:

Primera Parte: Sistemas y procesos multivariables

Segunda parte: Interacción entre variables dinámicas

Cuarta parte: Procedimiento de diseño de un sistema de control multivariable (primer acercamiento)

Referencias

Luyben, W. L., & Luyben, M. L. (1997). Essentials of Process Control. Singapore: McGraw-Hill.