Modelos matemáticos de sistemas dinámicos

Una de las herramientas más importantes de la representación de modelos lineales de parámetros agrupados de entrada-salida es la Función de Transferencia. La idea de emplear funciones de transferencia para representar sistemas es una consecuencia del uso de la transformada de Laplace para resolver ecuaciones diferenciales lineales.

Modelos lineales de sistemas dinámicos en tiempo continuo

Para comprender cómo se emplean las funciones de transferencia en la representación de una planta, supóngase que se tiene una planta general de n-ésimo orden, con una entrada u(t) y una salida y(t). Se puede obtener una aproximación del comportamiento de los sistemas físicos por medio de la solución de una ecuación diferencial lineal e invariante en el tiempo de n-ésimo orden que relacione la entrada y la salida. La forma general de dicha ecuación está dada por:

(1)

donde todas las a_i y c_i son constantes. Si se aplica la transformada de Laplace a la ecuación anterior, considerando que las condiciones iniciales son cero, se obtiene:

(2)

Agrupando, se tiene:

(3)

La función de transferencia Gp(s) del sistema se define como la relación entre la transformada de Laplace de la respuesta o salida del sistema Y(s) y la transformada de Laplace del estimulo o entrada U(s) correspondiente, por lo que se tiene la expresión:

(4)

Se dice que la función de transferencia Gp(s) tiene n polos y m ceros, los cuales desempeñan un papel muy importante en la determinación del carácter del comportamiento del sistema. En funciones de transferencia de los sistemas físicos reales, la potencia más alta de s en el numerador nunca es mayor a la del denominador; en otras palabras, n > m, ya que el sistema debe satisfacer la condición de causalidad, es decir, que ninguna de sus partes internas puede responder a entradas que aún no han ocurrido.

La función de transferencia Gp(s) caracteriza completamente al sistema, debido a que contiene toda la información referente a los coeficientes de la ecuación diferencial original que lo describe. Además, la función de transferencia depende solamente del sistema en sí, relacionando las transformadas de las variables de entrada con las de salida, a partir de algún estado inicial estacionario; de lo contrario, las condiciones iniciales que no son cero originan términos adicionales en la transformada de la variable de salida.

También es posible una descripción en modelos lineales dinámicos que caracterizan a los estados internos del sistema, en su descripción en espacio de estados

(5)

Donde , , son los vectores de estado, entrada y salida respectivamente y los vectores y son el ruido del proceso y de la medición.

Modelos lineales discretos de sistemas dinámicos

La forma general de representar la estructura de un modelo lineal discreto de entrada-salida es (Ljung, 1987):

y(t)=G(q^-1)u(t)+H(q^-1)e(t) (6)

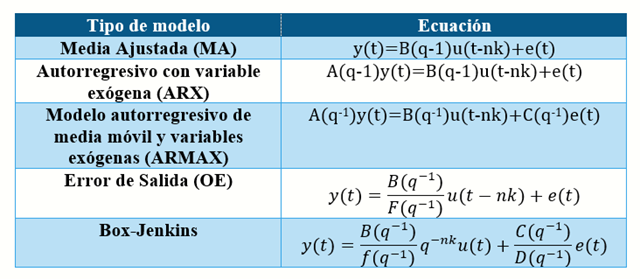
Los errores de modelización se incluyen en el término e(t). A este término se le asocia una serie de variables aleatorias independientes uniformemente distribuidas de media nula conocida como ruido blanco. Los términos G(q^-1) y H(q^-1) son funciones de transferencia de orden finito, que modelan la parte determinista y la parte estocástica respectivamente. Una característica de las distintas estructuras derivadas de (5) es la forma de modelar la parte estocástica o ruido. Una clasificación de estos modelos se presenta en la Tabla 4. Existen otros modelos lineales discretos dinámicos para representar a sistemas, los que se presentan son solo una muestra de los modelos disponibles.

Tabla 4: Modelos discretos lineales de entrada-salida (Ljung, 1987)

Nota: los términos A,B,C,D y F suelen ser polinomios en la variable q^-1

Modelos no lineales de sistemas dinámicos

Para un sistema no lineal cuya dependencia de las entradas pasadas disminuye rápidamente en el tiempo, puede expresarse una relación de entrada-salida descrita como serie de Volterra según

(7)

Donde y representan la entrada y la salida del sistema respectivamente y representa el núcleo de Volterra (Bergamasco & Lovera, 2010). El modelo representado en (7) es un modelo no lineal. El modelo de Volterra puede utilizarse para describir a procesos cuyo comportamiento no presente múltiples estados estacionarios ni comportamientos caóticos (Zhang, Chen, Wang, Li, & Qin, 2006). Existen muchos otros tipos de modelos no lineales, y depende de la naturaleza del sistema y su descripción.

Referencias

Bergamasco, M., & Lovera, M. (2010). Continuous-time predictor-based subspace identification using Laguerre filters. IET Control Theory and Applications, 5(7), 856-867.

Ljung, L. (1987). System identification: Theory for the user. New York: Prentice-Hall, Inc.

Zhang, H., Chen, Z., Wang, Y., Li, M., & Qin, T. (2006). Adaptive predictive control algorithm based on Laguerre Functional Model. International Journal of Adaptive Control and Signal Processing(20), 53-76.